Como o matemático adolescente Hannah Cairo refutou uma grande conjectura em análise harmônica

Quando Hannah Cairo tinha 17 anos, ela refutou a conjectura de Mizohata-Takeuchi, um palpite de longa data no campo da análise harmônica sobre como as ondas se comportam em superfícies curvas. A conjectura foi colocada na década de 1980, e os matemáticos tentavam provar isso desde então. Se a conjectura de Mizohata-Takeuchi fosse verdadeira, isso iluminaria muitas outras questões significativas no campo. Mas depois de atingir a parede após a parede tentando provar isso, o Cairo conseguiu criar um contra -exemplo: uma circunstância em que as ondas não se comportam como previsto pela conjectura. Portanto, a conjectura não pode ser verdadeira.
O Cairo ficou viciado no problema depois de receber uma versão mais simples da conjectura para provar como uma tarefa de casa para uma aula que ela estava fazendo na Universidade da Califórnia, Berkeley. “Demorei um pouco para convencer (instrutor do curso) Ruixiang Zhang de que minha proposta estava realmente correta”, diz ela. Agora, sob o aviso de Zhang, ela tem um artigo sobre o servidor pré -impressão arxiv.org e foi convidado a apresentar seus resultados na Conferência Internacional sobre Análise Harmônica e equações diferenciais parciais em El Escorial, Espanha.

Sobre apoiar o jornalismo científico
Se você está gostando deste artigo, considere apoiar nosso jornalismo premiado por assinando. Ao comprar uma assinatura, você está ajudando a garantir o futuro das histórias impactantes sobre as descobertas e idéias que moldam nosso mundo hoje.
Cairo diz que adora falar sobre sua pesquisa e fazer apresentações com slides coloridos e descritivos (Veja os exemplos abaixo). Quando perguntada sobre o que ela estuda, o Cairo diz, em suma, “pontos, linhas e ondas”.
Nascida e criada nas Bahamas, o Cairo se mudou para a Califórnia aos 16 anos, onde começou a ter aulas na UC Berkeley. Agora, aos 18 anos, ela está em Ph.D. Programa da Universidade de Maryland para continuar sua pesquisa na teoria da restrição de Fourier. Cairo enfrentou muitas dificuldades em sua jornada, mas encontrou conforto e pertencimento ao campo da matemática e no próprio trabalho.
Scientific American Falei com o Cairo sobre o modo como a análise harmônica é como colocar pedras em um lago parado, sua identidade transgênero e as razões que ela adora matemática.
(Uma transcrição editada da entrevista segue.)
Além de “pontos, linhas e ondas”, como você explicaria seu campo de estudo, análise harmônica?
Imagine que você está em um lago, e é um lago muito parado, e você solta uma pedra nela. Você vê essas ondas circulares se espalhando.
Se você soltar duas pedras na lagoa, poderá notar esse padrão chamado padrão de interferência: em vez de parecer círculos, eles se sobrepõem. Você recebe pontos altos, pontos baixos. E você obtém essas formas interessantes (onde elas se cruzam). E se você usasse um monte de ondulações – então o que você receberia? Na análise harmônica, você pode realmente provar que, se soltar suas pedras no lugar certo na lagoa, poderá obter qualquer forma que desejar.

Deslize da apresentação de Hannah Cairo sobre a conjectura de Mizohata-Takeuchi
Minha especialidade é conhecida como teoria de restrição de Fourier, que é a subdisciplina da análise harmônica em que trabalho, onde perguntamos em que tipo de objetos podemos construir se só podemos usar certos tipos de ondas. E se tivermos permissão para soltar as pedras em certas partes da lagoa? Você não será capaz de obter apenas nenhum objeto. Na verdade, você só poderá obter uma família relativamente pequena de objetos. O que a conjectura de Mizohata-Takeuchi diz é que a forma dos objetos que obtemos está concentrada ao longo das linhas.
O que significa estar “concentrado ao longo das linhas”?
Uma maneira de pensar na forma dos objetos é perguntar: o que é curvatura? Existem algumas maneiras diferentes de defini -lo. Uma maneira possível é tomar um retângulo fino e longo e perguntar quanto do seu círculo pode estar neste retângulo fino. O que você encontrará é que não é muito disso, porque se afasta, certo? Por outro lado, se você tomar algo plano como a borda de um quadrado, poderá obter um lado inteiro daquele quadrado apenas em um tubo fino. Então isso significa que o quadrado não é tão “curvado” quanto um círculo.
Para a conjectura de Mizohata-Takeuchi, dizemos, considere esse objeto que estamos construindo dessas ondas. E queremos dizer que não muito não vai mentir em formas que não contêm muitas linhas ou retângulos finos.
Então, como você conseguiu refutar essa conjectura?
Eu olhei para essas formas, e uma coisa que percebi é que o tipo específico de ondas usadas está concentrado ao longo de retângulos grossos. Na verdade, isso é algo bem conhecido. Então você acaba olhando para essas ondas que estão concentradas em retângulos: você pega essas ondas e elas se cruzam, e elas fazem essas formas, mas aqui (em vez de ondas circular), usamos ondas de retângulo. Então, temos todas essas ondas de retângulo se encontrando. O que eu percebi é que a forma de onde eles se encontram não está no ângulo certo para concordar com a direção em que esses retângulos estão apontando. E isso me levou a uma construção bastante complicada usando fractais para organizar esses retângulos.
A construção fractal original não aparece no seu artigo. Qual foi o seu contra -exemplo final?
O que eu descobri é que, se você organiza essas ondas, ocupando um hipercubo de alta dimensão e projetando-o para o espaço menor dimensional e depois pegando apenas as ondas que estão em sua região, é assim que você pode determinar onde colocá-las (para quebrar a conjectura).
O que o interessou pela primeira vez em matemática?
Eu sempre me interessei por matemática. Eu acho que, para mim, a matemática é uma arte. Na minha infância, eu estava um pouco solitária. A matemática estava quase como um amigo. Eu acho que a arte não pode necessariamente ser um amigo de todas as maneiras que um amigo pode ser, mas acho que a arte é como um amigo. E assim, desde que me lembro, sempre amei a matemática.
Conte -me mais sobre como a matemática era um amigo para você. Eu acho que muitas pessoas não pensam em matemática como muito amigáveis.
Há uma analogia que eu gosto de fazer, que é para outra forma de arte: pintura. E acho que, se alguém tivesse uma aula de tinta, você poderia memorizar as datas e horários em que várias formas de tinta foram desenvolvidas – e talvez até quais tintas foram usadas por que os pintores. E então você pode descobrir quais processos você pode usar para determinar que tipo de tinta é. Eu imagino que isso seja útil na história da arte, mas isso não é arte … eu não devo dizer isso. Talvez haja uma arte para aprender sobre tinta. Não vou afirmar que não existe porque não estudo tinta. Mas acho que a matemática é um pouco assim – na escola, as pessoas aprendem (a versão matemática da) pintura; Eles não estão aprendendo sobre pintura.
A matemática é reconfortante para mim, porque é uma maneira de explorar – explorar idéias e pensar sobre elas e criar mais idéias a partir de outras idéias. O que é reconfortante nisso é que é independente do mundo de certa forma. Se estou tendo um dia triste, um dia feliz, se eu me mudar para Maryland (me mudei para Maryland), a matemática ainda está lá, e ainda é a mesma coisa. Também é apenas algo que pode ocupar minha mente.
Você me mencionou que é transgênero. Como isso afetou sua jornada?
Eu acho que provavelmente é mais relevante em minha jornada como pessoa do que como matemático. Ser trans me forçou a ver coisas sobre o mundo que talvez eu não teria visto. Isso me fez ver o mundo de maneira diferente e me fez ver as pessoas de maneira diferente e me fez me ver de maneira diferente.
Felizmente, na comunidade de matemática, acho que a maioria dos matemáticos está bem com pessoas trans. Eu acho que costumava ser mais significativo (no meu dia a dia) do que é agora. Hoje em dia não faz muita diferença.
Por que você decidiu ir ao registro agora como trans?
A visibilidade trans é importante. As pessoas têm idéias sobre quem são as pessoas trans, e acho que é melhor ampliar isso. Talvez eu também espere que as pessoas que pensem que as pessoas trans são “menos” do que as pessoas cisgêneros possam se encontrar questionando isso.
A outra coisa é que é bom para as pessoas trans saber que não estão sozinhas. Eu acho que parte do que ajuda as pessoas trans a perceber que são trans é saber que existem mais opções para quem você pode ser como uma pessoa trans. Isso é importante para mim.
Muito obrigado por compartilhar isso. Onde está seu lugar favorito para fazer matemática?
Se estou tentando ser produtivo ao escrever algo, gosto de estar na minha mesa e gosto de ouvir Bach. Se estou apenas tentando pensar em idéias, meu lugar favorito para fazer isso é em algum lugar onde não preciso prestar atenção a muito mais. Eu poderia estar sentado em algum lugar pensando em coisas, ou poderia dar um passeio lá fora.
Também gosto de conversar com outras pessoas sobre matemática, que é outro tipo de matemática. Eu realmente gosto de fazer apresentações sobre matemática. Eu tenho esses slides manuscritos com todas essas cores e desenhos. Felizmente, na análise harmônica, posso fazer uma apresentação como essa, e então todo mundo está tão feliz, e eles me dizem que meus slides são fofos.
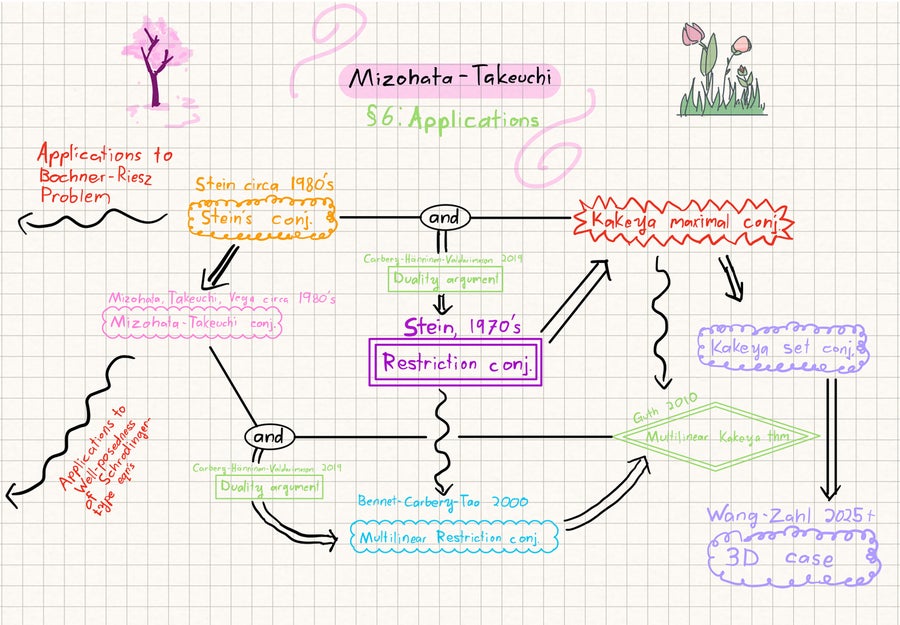
O slide final da apresentação do Cairo na conjectura de Mizohata-Takeuchi
O que vem a seguir para sua pesquisa?
Estou trabalhando em um projeto de pesquisa com meu consultor sobre mizohata-takeuchi e coisas adjacentes e sobre uma espécie de coisa diferente: o local Conjectura de Mizohata-Takeuchi.
O processo de aprender mais sobre esse tipo de matemática é bastante emocionante – não apenas para eu aprender mais sobre o que está por aí, mas para a comunidade de matemática como um todo tentar entender melhor esse tipo de coisa. (Isso é) algo que estou animado.




